Parabol Tepe Noktası Formülü ve Örnekleri

Parabol konusu öğrencilerin en çok zorlandığı konulardan bir tanesidir. Bu yüzden bol tekrar ve soru çözümü gerektirmektedir. Parabol konusundan AYT sınavında her sene 1 soru gelebilmektedir. Bu yazımızda tepe noktası formülü üzerine bir yazı hazırladık. Formülün mantığını öğrenebilir ve örneklerle konuyu pekiştirebilirsiniz.

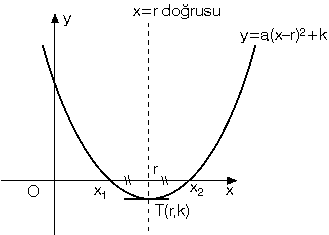
Tepe Noktası Formülü

f(x) = a.(x-r)² + k biçimindeki ikinci dereceden bir değişkenli fonksiyonun (parabolün) tepe noktası T(r,k) ise

r = −b/2a ve k = f(r) = (4ac-b²)/4a’dır ve bunlar biliniyorsa f(x) = a.(x−r)² + k parabol denklemi yazılabilir.

Örnek 1: f(x) = 5.(x+4)²+9 parabolünün tepe noktası nedir?

Çözüm: Formüle baktığımızda x-r = x+4 olması gerektiğinden dolayı r=-4 çıkar. k ise sabit değer olur. Yani k=9 çıkmaktadır. Buna göre parabolün tepe noktası T(-4,9) çıkmaktadır.

Örnek 2: f(x) = 3x² + 18x parabolünün tepe noktası nedir?

Çözüm: Burada r= -b/2a formülünü kullanmamız gerekmektedir. -18/6 dan r = -3 çıkar.
k = f(-3) = 3.(-3)² + 18.(-3) = -27 çıkmaktadır. Buna göre parabolün tepe noktası T(-3,-27) olur.

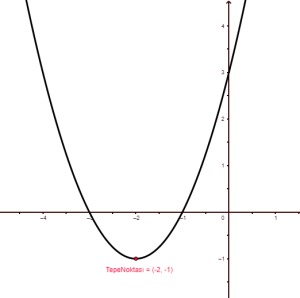
Örnek 3: x² + 4x + 3 parabolünün tepe noktası nedir?

Çözüm: Burada a = 1 ve b = 4 olur. Öyleyse -b / 2a da -4 / 2 = -2 olur. Demek ki r = -2 şeklindedir. Şimdi de k değerini bulmak için -2’yi denklemde yerine yazalım. (-2)² + 4.(-2) + 3 = -1 bulunur. Bulduğumuz şey k değeridir. Öyleyse tepe noktası T(-2, -1) şeklindedir.

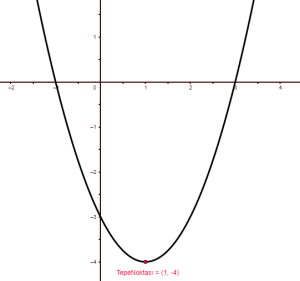
Örnek 4: x² – 2x – 3 parabolünün tepe noktası nedir?

Çözüm: Burada a = 1 ve b = -2 olur. Öyleyse -b / 2a da 2 / 2 = 1 olur. Demek ki r = 1 şeklindedir. Şimdi de k değerini bulmak için 1’i denklemde yerine yazalım. (1)² – 2.(1) – 3 = -4 bulunur. Bulduğumuz şey k değeridir. Öyleyse tepe noktası T(1, -4) şeklindedir.

Sizler için hazırladığımız tepe noktası formülü ve örnekleri yazısı bu şekildedir. Eklememizi istediğiniz formüller varsa yorum kısmında belirtebilirsiniz. Sitemizde bulunan integral alma kuralları yazısını da incelemeyi unutmayınız.