Çarpanlara Ayırma Formülleri + PDF

Çarpanlara Ayırma konusu bazı diğer konuları öğrenmen açısından da çok önemlidir. AYT Matematik yapabilmen için bu konuyu çok iyi bilmeniz gerekiyor.  Çünkü çarpanlara ayırma konusu parabolde, polinomda, 2. derecede denklemlerde, eşitsizliklerde, türevde, dizilerde ve diğer bazı konularda karşımıza bolca çıkacaktır. Bu yazımızda sizler için çarpanlara ayırma formüllerini paylaşıyoruz.

Çarpanlara Ayırma Formülleri

Son yıllarda direkt olarak çarpanlara ayırma konusundan çok soru gelmemiş olsa da diğer konularda karşımıza çıktığı için tam öğrenmeniz gerekmektedir.

Tam Kare Açılımı

• İki terimin toplamının karesi: (x + y)² = x² + 2xy + y²
• İki terimin farkının karesi: (x − y)² = x² − 2xy + y²
• Üç terimin toplamının karesi: (x + y + z)² = x² + y² + z² + 2.(xy + xz + yz)

İki Kare Farkı ve Toplamı

• x² – y² = (x + y).(x – y)
• x² + y² = (x + y)² – 2xy veya (x – y)² + 2xy

Küp Açılımı

• İki terimin toplamının küpü: (x + y)³ = x³ + 3x²y+ 3xy² + y³
• İki terimin farkının küpü: (x − y)³ = x³ − 3x²y + 3xy² − y³
• İki küp toplamı : x³ + y³ = (x + y).(x² – xy + y²)
• İki küp farkı : x³ − y³ = (x − y).(x² + xy + y²)

xⁿ + yⁿ veya xⁿ − yⁿ biçimindeki polinomların özdeşliği:

• x⁴ – y⁴ = (x² + y²).(x + y).(x – y)
• x⁵ + y⁵ = (x + y).(x⁴ – x³y + x² y² – xy³ + y⁴)
• x⁵ – y⁵ = (x – y).(x⁴ + x³y + x² y² + xy³ + y⁴)
• x⁶ – y⁶ = (x – y).(x² + xy + y²).(x+ y).(x² − xy + y²)
• x⁷ + y⁷ = (x + y).(x⁶ – x⁵y + x⁴y² – x³y³ + x²y⁴ – xy⁵ + y⁶)
• x⁷ – y⁷ = (x – y).(x⁶ + x⁵y + x⁴y² + x³y³ + x²y⁴ + xy⁵ + y⁶)

(x + y)’nin katları şeklindeki açılımlar;

• (x + y)⁴ = x⁴ + 4x³y + 6x²y² + 4xy³ + y⁴
• (x – y)⁴ = x⁴ – 4x³y + 6x²y² – 4xy³ + y⁴
• (x + y)⁵ = x⁵ + 5x⁴y + 10x³y² + 10x²y³ + 5xy⁴ + y⁵
• (x – y)⁵ = x⁵ – 5x⁴y + 10x³y² – 10x²y³ + 5xy⁴ – y⁵

Özdeşlikleri aşağıdaki şekilde düzenleyerek de kullanabiliriz:

• (x – y)² = (x + y)² – 4xy
• (x + y)² = (x – y)² + 4xy
• x³ – y³ = (x – y)³ + 3xy (x – y)
• x³ + y³ = (x + y)³ – 3xy (x + y)
• x² + y² + z² = (x + y + z)² – 2 (xy + xz + yz)

Ortak Çarpan Parantezine Alma

Toplama çıkarma durumunda verilen ifadelerin hepsinde ortak olarak bulunan en büyük çarpanın parantezine alınmasına ifadeleri ortak çarpan parantezine alma denir.

Ortak paranteze alma örneği şu şekildedir:

• ax + bx = x . (a + b)
• ax – bx = x . (a – b)
• 5.(x+y)=5x+5y
• x²y+y=y.(x²+1)

Gruplandırarak Çarpanlara Ayırma

Her bir terimde ortak çarpan yoksa ortak çarpanı olan terimler gruplandırılır.

Gruplandırma örneği şu şekilde olur:

• x² + ax + bx + ab = (x² + ax) + (bx + ab)
• x² + ax + bx + ab = x . (x + a) + b . (x + a)
• x² + ax + bx + ab = (x + b) . (x + a)

Örnek: xa + xb + ya + yb = x.(a+b) + y.(a+b) = (a+b).(x+y)

Önce x’leri kendi aralarında çarpanlarına ayırdık, daha sonra y’leri. a+b’nin ortak olduğunu gördük. a+b’yi parantez içine aldık, dışarda kalan elemen x+y’dir.

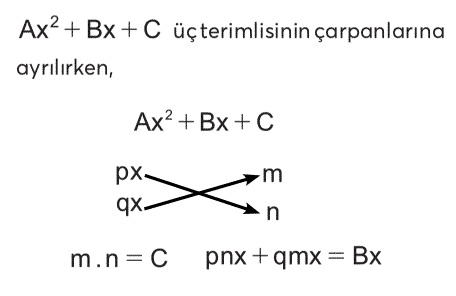
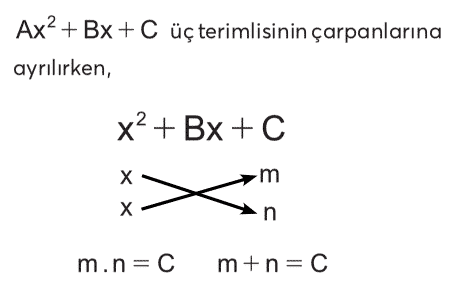
2. Derece Üç Terimlinin Çarpanlarına Ayrılması

Çarpanlara Ayırma PDF

Sizler için çarpanlara ayırma formülleri üzerine piyasada ücretsiz olarak değerli öğretmenlerimiz ve kurumlarımız tarafından paylaşılan PDF’leri derledik.

• Rehber Matematik Çarpanlara Ayırma
• Özel Öğrenci Çarpanlara Ayırma
• Matematiğin Güler Yüzü Çarpanlara Ayırma
• Laptü Matematik Çarpanlara Ayırma
• Selim Yüksel Bıyıklı Matematik Çarpanlara Ayırma

Bu güzel PDF notları için teşekkür ederiz.

Sizler için hazırladığımız çarpanlara ayırma formülleri bu şekildedir. Eklememizi istediğiniz formüller varsa yorum kısmında belirtebilirsiniz. Sitemizdeki diğer içerikleri incelemeyi unutmayınız.